
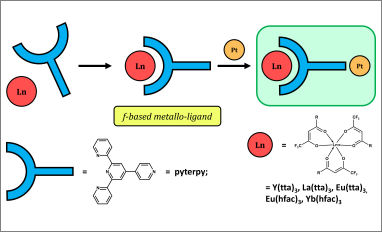
 Congratulations to our PhD student Marco Bazi for the recent scientific publication entitled “Mononuclear Rare-Earth Metalloligands Exploiting a Divergent Ligand” in Inorganic Chemistry. Seven Rare-Earth compounds with formula [RE(dike)3pyterpy] were synthesized using the divergent ligand “pyterpy” and two different ancillary ligands (dike= tta with Htta = 2-thenoyltrifluoroacetone or dike = hfac with Hhfac hexafluoroacetylacetone).
Congratulations to our PhD student Marco Bazi for the recent scientific publication entitled “Mononuclear Rare-Earth Metalloligands Exploiting a Divergent Ligand” in Inorganic Chemistry. Seven Rare-Earth compounds with formula [RE(dike)3pyterpy] were synthesized using the divergent ligand “pyterpy” and two different ancillary ligands (dike= tta with Htta = 2-thenoyltrifluoroacetone or dike = hfac with Hhfac hexafluoroacetylacetone).
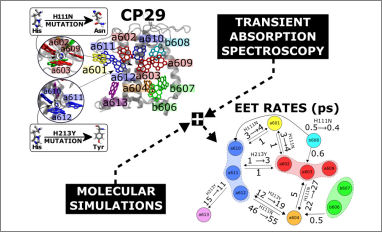 Congratulations to our PhD student Piermarco Saraceno for his publication titled "Probing the Effect of Mutations on Light Harvesting in CP29 by Transient Absorption and First-Principles Simulations" in The Journal of Physical Chemistry Letters. This research explores how mutations affect the energy transfer efficiency within the CP29 complex, a key component in plant photosynthesis. The study employs an advanced approach that combines ultrafast spectroscopy with first-principles simulations to reveal detailed excitation energy transfer (EET) pathways.
Congratulations to our PhD student Piermarco Saraceno for his publication titled "Probing the Effect of Mutations on Light Harvesting in CP29 by Transient Absorption and First-Principles Simulations" in The Journal of Physical Chemistry Letters. This research explores how mutations affect the energy transfer efficiency within the CP29 complex, a key component in plant photosynthesis. The study employs an advanced approach that combines ultrafast spectroscopy with first-principles simulations to reveal detailed excitation energy transfer (EET) pathways.
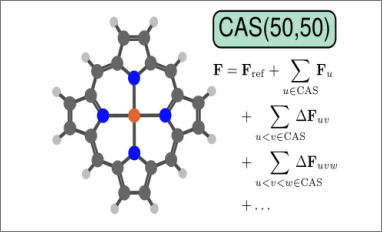 Congratulations to our PhD student Ivan Giannì and our Postdoctoral researcher Tommaso Nottoli for their publication entitled "MBE-CASSCF Approach for the Accurate Treatment of Large Active Spaces" in the Journal of Chemical Theory and Computation. The work presents a novel implementation of the complete active space self-consistent field (CASSCF) method that makes use of the many-body expanded full configuration interaction (MBE-FCI) method to incrementally approximate electronic structures within large active spaces.
Congratulations to our PhD student Ivan Giannì and our Postdoctoral researcher Tommaso Nottoli for their publication entitled "MBE-CASSCF Approach for the Accurate Treatment of Large Active Spaces" in the Journal of Chemical Theory and Computation. The work presents a novel implementation of the complete active space self-consistent field (CASSCF) method that makes use of the many-body expanded full configuration interaction (MBE-FCI) method to incrementally approximate electronic structures within large active spaces.
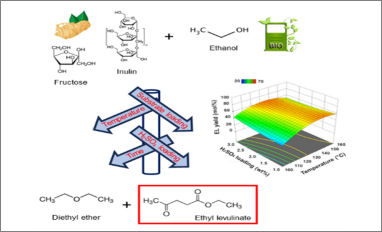 Congratulations to our PhD student Lorenzo Bonaldi for his scientific publication entitled “In-depth Investigation of the Reaction Parameters Tuning the Ethyl Levulinate Synthesis from Fructose and Inulin”. Alkyl levulinates (ALs) are strategic compounds for the development of sustainable energy transition. In this work, the direct alcoholysis of two model substrates (fructose and inulin) was investigated using a One-Factor-At-a-Time (OFAT) approach for the selective production of ethyl levulinate (EL), with diluted H₂SO₄ as the catalyst.
Congratulations to our PhD student Lorenzo Bonaldi for his scientific publication entitled “In-depth Investigation of the Reaction Parameters Tuning the Ethyl Levulinate Synthesis from Fructose and Inulin”. Alkyl levulinates (ALs) are strategic compounds for the development of sustainable energy transition. In this work, the direct alcoholysis of two model substrates (fructose and inulin) was investigated using a One-Factor-At-a-Time (OFAT) approach for the selective production of ethyl levulinate (EL), with diluted H₂SO₄ as the catalyst.



